Table Of Contents
Previous topic
Next topic
This Page
Quick search
Enter search terms or a module, class or function name.
- normalize_set()
- normalize a set of vectors
- orthogonalize_set()
- orthogonalize a set of vectors
- contract()
- double contract of two arrays
- contract_t()
- double contract a second-rank tensor
- rotate_t()
- rotate a second-rank tensor
- norm()
- norm of an array
- cosine()
- cosine between two arrays
- mass_center()
- coordinates of the mass center
- inertia_tensor()
- inertia tensor
- rotmatrix_axis()
- matrix for rotation about an arbitrary axis
- quat2matrix()
- left rotation matrix from a normalized quaternion
- calc_dcm()
- direction cosine matrix
- levi_civita()
- antisymmetric unit tensor of Levi-Civita
- is_even_permutation()
- determine whether a permutation is even
- kronecker()
- kronecker symbol
- decompose()
- decompose a 3x3 matrix
- decompose_t()
- decompose a second-rank tensor
- crossproduct()
- cross product of two vectors
- spatproduct()
- scalar triple product of three vectors
- angle_vectors()
- angle between vectors
- distance()
- distance between two points
- angle()
- angle between three points
- dihedral()
- dihedral angle between four points
- make_gcm()
- generate a group coupling matrix (GCM)
- make_gcp()
- generate group contribution patterns (GCPs)
- boltzmann_distr()
- Boltzmann energy distribution of molecules
- signum()
- signum
- fitgauss_params()
- fitting a Lorentz function with Gaussian functions
- voigt_norm()
- normalized approximate Voigt profile
- boltzmann_factor()
- Boltzmann correction
- savitzky_golay()
- smooth data with the Savitzky-Golay algorithm
- apply_corr()
- apply a correction of a given order to a one-dimensional array
| Author: | Maxim Fedorovsky |
|---|
Normalize a set of vectors.
| Parameters: |
|
|---|
Orthogonalize a set of vectors using the Gram-Schmidt algorithm.
| Parameters: |
|
|---|
Double contract two arrays.
The double contraction of two arbitrary second-rank tensors
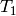 and
and 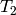 is given by:
is given by:
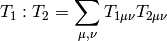
| Parameters: |
|
|---|
Double contract the elements of a second-rank tensor with themselves.
| Parameter: | tens – second-rank tensor (one-based ndarray), shape: (1 + N, 4, 1 + N, 4) with N being the number of atoms |
|---|---|
| Returns: | a tuple with the total contraction and the isotropic, anisotropic and antisymmetric contributions. |
Rotate a second-rank tensor.
Each dinuclear term  of such a tensor
of such a tensor 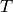 is rotated with
a rotation matrix
is rotated with
a rotation matrix 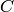 as follows:
as follows:
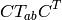
| Parameters: |
|
|---|
Calculate the norm of an array.
The norm is considered to be the square root of the double contraction of the array with itself. The array can be multi-dimensional such as e.g. tensors.
| Parameter: | ar (ndarray) – array |
|---|
See also
Calculate the cosinus between two arrays.
Teh cosine is considered to be the result of the double contraction of the arrays divided by the product of their norms.
| Parameters: |
|
|---|
Calculate the mass center.
| Parameters: |
|
|---|
Calculate the inertia tensor.
| Parameters: |
|
|---|---|
| Returns: | inertia tensor as a null-based two-dimensional ndarray |
Generate a matrix of rotation about an arbitrary axis.
| Parameters: |
|
|---|
The result rotation matrix is a one-based two-dimensional ndarray.
Generate a left rotation matrix from a normalized quaternion.
| Parameter: | quat (null-based array of the length 4) – normalized quaternion |
|---|
The result matrix is a one-based two-dimensional ndarray.
Calculate the direction cosine matrix between two coordinates systems.
| Parameters: |
|
|---|
The result matrix is a one-based two-dimensional ndarray.
Antisymmetric unit tensor of Levi-Civita.
/- +1 if (i,j,k) is an even permutation of (1,2,3)
eps(i,j,k) = | -1 if (i,j,k) is an odd permutation of (1,2,3)
\- 0 if at lease two indices are equal
The result tensor is a one-based three-dimensional ndarray.
Determine whether a permutation is even.
An even permutation is a permutation that can be produced by an even number of exchanges.
| Parameter: | perm (tuple) – permutation |
|---|
Kronecker symbol.
/- 1 if i = j
delta(i,j) = |
\- 0 otherwise
| Parameters: |
|
|---|
Decompose a matrix into the isotropic, anisotropic & antisymmetric part.
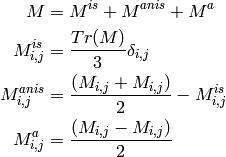
| Parameter: | mat (one-based ndarray with shape (4, 4)) – matrix to be decomposed () |
|---|---|
| Returns: | tuple with the isotropic, anisotropic and antisymmetric parts |
Decompose a second-rank tensor into the isotropic, anisotropic and antisymmetric part.
| Parameter: | tens – second-rank tensor to be decomposed (one-based ndarray) shape: (1 + N, 4, 1 + N, 4) with N being the number of atoms |
|---|---|
| Returns: | tuple with the parts |
See also
Calculate the cross-product of two vectors.
| Parameters: |
|
|---|
Calculate the scalar triple product of three vectors.
| Parameters: |
|
|---|
Calculate the angle between two vectors.
| Parameters: |
|
|---|---|
| Returns: | the angle in grad |
Calculate the distance between two points.
| Parameters: |
|
|---|
Calculate the angle between three points.
| Parameters: |
|
|---|---|
| Returns: | the angle in grad |
Calculate the dihedral angle between four points.
| Parameters: |
|
|---|---|
| Returns: | the dihedral angle in grad |
Generate a group coupling matrix (GCM).
The GCM is obtained by separately adding up intra-group mono- and di-nuclear terms, and inter-group di-nuclear terms.
For details refer to W. Hug. Chem. Phys., 264(1):53-69, 2001.
| Parameters: |
|
|---|---|
| Returns: | the GCM with shape (1 + N_gr, 1 + N_gr) with N_gr being the number of groups. |
Generate group contribution patterns (GCPs).
The GCPs are obtained by adding the contributions of atoms comprising the groups.
For details refer to W. Hug. Chem. Phys., 264(1):53-69, 2001.
| Parameters: |
|
|---|---|
| Returns: | the GCP of the length 1 + N_gr with N_gr being the number of groups |
Calculate the Boltzmann energy distribution of molecules.
| Parameters: |
|
|---|---|
| Returns: | null-based ndarray with the percentages of the molecules (values between 0 to 1). |
Signum of a number.
/- 1 if x > 0
signum(x) = | 0 if x = 0
\- -1 otherwise
Parameters of a least square fitting Gauss functions to the shape of a Lorentz function with a full width at half-maximum (FWHM) of 1.
For details refer to W. Hug and J. Haesler. Int. J. Quant. Chem. 104:695-715, 2005
| Parameter: | n_gauss – number of Gauss functions, currently the supported range of values is between 3 and 8 |
|---|---|
| Returns: | ndarray of the dimension (2, n_gauss), each column of which corresponds to pair (c_i, a_i). |
Normalized approximate Voigt profile as a combination of Gauss functions.
For details refer to W. Hug and J. Haesler. Int. J. Quant. Chem. 104:695-715, 2005
| Parameters: |
|
|---|
Boltzmann correction.
The correction takes into account the thermal population of vibrational states. It is applied to the Raman/ROA scattering cross-sections, since they depend on the temperature at which a sample is measured.
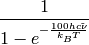
| Parameter: | wavnu – wavenumber in cm**(-1) |
|---|
Smooth data with the Savitzky-Golay algorithm.
The returned smoothed data array has the same dimension as the original one.
| Parameters: |
|
|---|
Apply a correction of a given order to one-dimensional array.
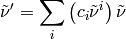
| Parameters: |
|
|---|---|
| Returns: | the corrected array as given above |
