Table Of Contents
Previous topic
Next topic
This Page
Quick search
Enter search terms or a module, class or function name.
The formulae used to implement this module have been taken from [1].
References
| [1] | W. Hug. Chem. Phys., 264(1):53-69, 2001, [ doi: 10.1016/S0301-0104(00)00390-6 ] |
| [2] | (1, 2) W. Hug and J. Haesler, Int. J. Quant. Chem. 104:695-715, 2005, [ doi: 10.1002/qua.20600 ] |
| [3] | Atkins, 6th edition, p. 459. |
- RamanROATensors
- manipulating the Raman/ROA tensors
- IRVCDTensors
- manipulating the IR/VCD tensors
- ExpRamanROAData
- experimental Raman, ROA or Degree of circularity spectra
- contract_A_tensor()
- contract the derivatives of the A tensor
- f_Qp_i()
- transition integral between two states
- Kp()
- constant Kp used for the Raman/ROA cross-sections
- conv_units_raman_roa()
- convenience function for conversions
- conv_invariant()
- conversion: a.u. -> invariants’ units
- conv_cross_sections()
- conversion: a.u. -> cross-section’ units
- conv_A4_AMU()
- conversion: a.u. -> A^4 / AMU
- inv_coeffs_raman_roa()
- linear combinations for the cross-sections
- stick_raman_roa()
- generate Raman/ROA stick spectra
- fit_raman_roa()
- generate Raman/ROA spectra as curves
- make_acp()
- generate atomic contribution patterns (ACPs)
- calc_spectra_nmol()
- calculate VROA spectra for several molecules
- LIST_INVARIANTS
- list of available invariants
- LIST_VTENSORS
- list of available V tensors
- LIST_INVARIANTSUNITS
- list of available units of the invariants (J)
- X_PEAK_INTERVAL
- length of a peak’s fitting interval
- X_STEP
- default x step for fitting curves
| Author: | Maxim Fedorovsky |
|---|
Class for manipulating the Raman/ROA tensors.
Refer to the DALTON manual page for information how to request a ROA job. http://www.kjemi.uio.no/software/dalton/resources/dalton20manual.pdf
 molecular invariant
molecular invariant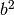 molecular invariant
molecular invariant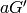 molecular invariant
molecular invariant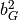 molecular invariant
molecular invariant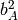 molecular invariant
molecular invariant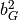 and
and 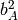 invariants
invariants molecular invariant
molecular invariant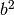 molecular invariant
molecular invariant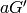 molecular invariant
molecular invariant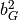 molecular invariant
molecular invariant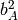 molecular invariant
molecular invariantInitializer of the class.
PP, Lx, freqs and lambda_incident are required to be set. If PM or PQ are not set, they will be filled with zeros.
| Parameters: |
|
|---|
Calculate the five molecular invariants for all vibrations.
A row is made up of  ,
, 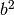 ,
, 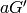 ,
,
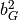 and
and 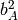 .
.
| Parameters: |
|
|---|---|
| Returns: | zero-based ndarray with a shape of (NFreq, 5) with NFreq being the number of vibrations. |
Calculate the five molecular invariants for all vibrations taking into account the contributions of groups A and B.
A row is made up of  ,
, 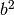 ,
, 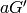 ,
,
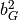 and
and 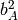 .
.
| Parameters: |
|
|---|---|
| Returns: | zero-based ndarray with a shape of (3, NFreq, 5) with NFreq being the number of vibrations. The first index refers to the contribution of AA (0), AB(1) and BB(2). |
Decompose the five molecular invariants for all vibrations.
A row is made up of  ,
, 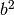 ,
, 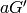 ,
,
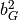 and
and 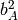 with a shape
of (nparts, nparts) where nparts is the number of parts.
with a shape
of (nparts, nparts) where nparts is the number of parts.
| Parameters: |
|
|---|---|
| Returns: | ndarray with a shape of (NFreq, 5, nparts, nparts) with NFreq being the number of vibrations. |
Get the five molecular invariants for a given molecule.
| Parameters: |
|
|---|
Calculate the five reduced molecular invariants for the rotations.
A row is made up of  ,
, 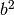 ,
, 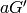 ,
,
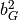 and
and 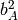 .
.
| Parameters: |
|
|---|
Lx_rot can be obtained as follows:
Lx_rot = mol.Lx_tr_rot[1 + mol.nrot:]
| Returns: | zero-based ndarray with the shape of (nrot, 5) with nrot being the number of rotations. |
|---|
Calculate the V-tensor for the  molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
The tensor is expressed in a.u.
Calculate the V-tensor for the 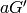 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
The tensor is expressed in a.u.
Calculate the five V-tensors from passed gradients.
| Parameters: |
|
|---|---|
| Returns: | V_a2, V_b2, V_aG, V_b2G, V_b2A |
Calculate the V-tensor for the 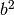 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
The tensor is expressed in a.u.
Calculate the V-tensor for the 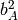 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
The tensor is expressed in a.u.
Calculate the V-tensor for the 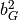 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
The tensor is expressed in a.u.
Calculate the spacial term for 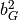 and
and 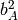 .
.
| Parameter: | i – part of the decomposed tensor (default 0, i.e. total sum) possible values:
|
|---|
The tensor is expressed in a.u.
Calculate the  molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
Calculate the 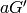 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
Generate atomic contribution patterns (ACPs).
See also make_acp().
| Parameters: |
|
|---|
The ACPs have a unit of cross-sections for raman, roa_* etc. and that of invariants for single invariants.
Calculate the 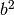 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
Calculate the 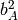 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
Calculate the 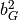 molecular invariant.
molecular invariant.
| Parameters: |
|
|---|
Calculate fitted spectra.
| Parameters: |
|
|---|
a = ab[0]
b = ab[1]
new_freqs = (a * freqs + b) * freqs
| Parameters: |
|
|---|---|
| Returns: | X, raman_Y, roa_Y, degcirc_Y |
Generate group contribution patterns (GCPs).
| Parameters: |
|
|---|
The GCPs have a unit of cross-sections for raman, roa_* etc. and that of invariants for single invariants.
Calculate the Raman/ROA intensities.
| Parameters: |
|
|---|
Calculate the normalized sum of ROA over the rotations.
See eq 33 in [2].
| Parameters: |
|
|---|
Calculate the normalized sum of ROA over a range of vibrations.
It is a measure of the influence of the chiral distribution of a molecule’s electrons on vibrational ROA alone.
See eq 34 in [2].
| Parameters: |
|
|---|---|
| Returns: | freqs, roa_cumsum having a length of end_p - start_p + 1 |
Overwrite the V-tensors generated from the gradients.
| Parameter: | V_tensors – list or tuple with V_a2, V_b2, V_aG, V_b2G, V_b2A, each of which is a ndarray with a shape of (1 + Natoms, 4, 1 + Natoms, 4) |
|---|
An exception is raised unless the V-tensors are valid.
Calculate stick spectra.
| Parameters: |
|
|---|---|
| Returns: | X, raman_Y, roa_Y, degcirc_Y. Each of these arrays is zero-based and of the length NFreq. |
Perform a geometrical transformation.
New origin must be given if a translation of the origin dependent gradients of the G’ and A tensors is desired.
| Parameters: |
|
|---|
The coordinates are assumed to be given in angstroms.
Class for manipulating the IR/VCD tensors.
Refer to the DALTON manual page for information on how to request a VCD job, http://www.kjemi.uio.no/software/dalton/resources/dalton20manual.pdf
Initializer of the class.
P, Lx and freqs are required to be set. If M is not set, it will be filled with zeros.
| Parameters: |
|
|---|
Calculate the matrix of the reduced dipole strength.
| Parameter: | p – number of vibration |
|---|
Calculate the matrix of the reduced rotational strength.
| Parameter: | p – number of vibration |
|---|
Generate atomic contribution patterns (ACPs).
| Parameters: |
|
|---|
See also
Generate the IR/VCD spectra as curves.
| Parameters: |
|
|---|
a = ab[0]
b = ab[1]
new_freqs = (a * freqs + b) * freqs
| Parameter: | groups_AB – unless None, defines two groups A and B whose contributions are to be used for calculating the spectra, format : [group_A, group_B, t] t = 0 for AA, 1 for AB + BA and 2 for BB |
|---|---|
| Returns: | X, eps_Y, deps_Y, g_Y |
Get the integrated absorption coeffcients (in SI) and the g-factors.
The shape of the bands is considered to be Lorentzian.
| Parameter: | groups_AB – unless None, defines two groups A and B whose contributions are to be used for calculating the spectra, format : [group_A, group_B, t] t = 0 for AA, 1 for AB + BA and 2 for BB |
|---|
See [3].
| Returns: | ndarray with a shape of (NFreq, 3) |
|---|
Calculate the matrix of the infrared absorption intensity.
| Parameter: | p – number of vibration |
|---|
The units are m/mol.
Calculate the normalized sum of VCD over the rotations.
| Parameter: | masses – masses of the atoms in AMU (one-based ndarray), shape: (1 + Natoms,) |
|---|
Calculate the normalized sum of VCD over a range of vibrations.
| Parameters: |
|
|---|---|
| Returns: | freqs, roa_cumsum having a length of end_p - start_p + 1 |
Perform a rotation.
| Parameter: | rotmat (ndarray, shape: (4, 4)) – rotation matrix |
|---|
Calculate the matrix of the VCD intensity.
| Parameter: | p – number of vibration |
|---|
The units are m/mol.
Storing experimental Raman, ROA or Degree of circularity spectra.
Initializer of the class.
| Parameters: |
|
|---|
Contract the derivaritives of the A tensor.
The contraction with antisymmetric unit tensor of Levi-Civita
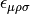 is performed
using the following formula (the Einstein summing convention of indices
is used):
is performed
using the following formula (the Einstein summing convention of indices
is used):
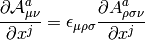
| Parameter: | A – derivaritives of the A tensor (one-based ndarray), shape: (1 + Natoms, 4, 4, 4, 4) with Natoms being the number of atoms |
|---|---|
| Returns: | the derivatives of the  tensor with a shape of
(1 + Natoms, 4, 4, 4) tensor with a shape of
(1 + Natoms, 4, 4, 4) |
See also
Transition integral between two vibrational states
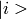 and
and  .
.
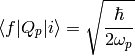
It is assumed that the f <- i is a fundamental transition and that the vibration is harmonic.
| Parameter: | nu – wavenumber in cm**(-1) |
|---|
Return value is expressed in SI units.
Factor appearing in the calculating of the Raman/ROA cross-sections.
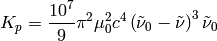
| Parameters: |
|
|---|
Return value is expressed in SI units.
Conversion factor for a Raman/ROA quantity.
| Parameters: |
|
|---|
Conversion factor from J_ab in a.u. to molecular invariants in SI units.
| Parameter: | nu – wavenumber in cm**(-1) |
|---|
Conversion factor from J_ab in a.u. to the cross-sections in A^2 / sr.
| Parameters: |
|
|---|
Conversion factor from J_ab in a.u. to A^4/AMU.
For a2 and b2 (Raman invariants) : 142.943570. For aG, b2G, b2A (ROA invariants): 142.943570 / C_AU, with C_AU being the speed of light in a.u.
| Parameter: | J – molecular invariant, one of (‘a2’, ‘b2’, ‘aG’, ‘b2G’, ‘b2A’) |
|---|
Linear combination coefficients of the five molecular invariants for the Raman/ROA cross-sections for a given scattering type.
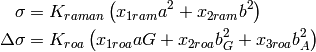
| Parameter: | scattering – scattering, the default one is backward |
|---|
Possible values of the scattering argument:
- 0: backward ( 1., 90., 14., 4./C_AU, 0., 12., 4.)
- 1: forward ( 1., 90., 14., 4./C_AU, 90., 2., -2.)
- 2: 90_perp ( 1., 45., 7., 2./C_AU, 45., 7., 1.)
- 3: 90_par ( 1., 0., 6., 2./C_AU, 0., 6., -2.)
- 4: integral (4*pi/3., 180., 40., 8*pi/3./C_AU, 180., 40., 0.)
where C_AU is the speed of light in a.u.
| Returns: |  |
|---|
Generate Raman/ROA stick spectra.
| Parameters: |
|
|---|---|
| Returns: | X, raman_Y, roa_Y, degcirc_Y. Each of these arrays is zero-based and of the length NFreq. |
Generate Raman/ROA spectra as curves.
| Parameters: |
|
|---|---|
| Returns: | X, raman_Y, roa_Y, degcirc_Y |
Generate atomic contribution patterns (ACPs).
| Parameters: |
|
|---|---|
| Returns: | the ACPs as a one-based ndarray |
Calculate VROA spectra for several molecules.
| Parameters: |
|
|---|---|
| Returns: | dictionary with the following keys:
|
